Deep Latent Variable Models

LVMs has been usually restricted to the conjugate exponential family because, in this case, the inference was feasible (and scalable). But recent advances in variational inference are inspiring many recent works extending LVMs with DNNs. Variational Auto-encoders (VAE) [@kingma2013auto; @doersch2016tutorial] are probably the most influential work combining LVMs and deep neural networks. VAEs extend the classic technique of principal component analysis (PCA) [@jolliffe2011principal] for data representation in lower-dimensional spaces. More precisely, [@kingma2013auto] extends the probabilistic version of the PCA model [@tipping1999probabilistic] where the relationship between the low-dimensional representation and the observed data is governed by a DNN, i.e. a highly non-linear function, as opposed to the standard linear assumptions of the basic version of the PCA model. These new models were able to capture much more compact low-dimensional representation especially in cases where data were highly-dimensional and complex¹. As it is the case of image data [@kingma2013auto; @kulkarni2015deep; @gregor2015draw; @sohn2015learning; @pu2016variational], text data [@semeniuta2017hybrid], audio data [@hsu2017learning], chemical molecules [@gomez2018automatic], to name some of the most representative applications of this technique.

As commented above, VAEs have given rise to a plethora of extensions of classic LVMs to their deep countepart. [@johnson2016composing] contains different examples of this approach and proposes extensions of Gaussian mixture models, latent linear dynamical systems and latent switching linear dynamical systems with non-linear relationships modelled by DNNs. [@linderman2016recurrent] extends hidden semi-Markov models with recurrent neural networks. [@zhou2015poisson; @card2017neural] extends popular LDA models [@blei2003latent] for uncovering topics in text data. Many other works are following this same trend [@chung2015recurrent; @jiang2016variational; @xie2016unsupervised; @louizos2017causal].

LVMs with DNNs can also be found in the literature under the name of deep generative models [@hinton2009deep; @hinton2012practical; @goodfellow2014generative; @salakhutdinov2015learning]. These models highlight their capacity to generate data samples using probabilistic constructs that include DNNs. This new capacity has also provoked a strong impact within the deep learning community because has opened the possibility of dealing with unsupervised learning problems, as opposed to the classic deep learning methods which were mainly focused on supervised learning settings. In any case, this active area of research is out of the scope of this post and contains many alternative models which do not fall within the category of models explored in this work [@goodfellow2014generative].

Probabilistic Programming Languages and Stochastic Computational Graphs

One of the main reasons fueling the wide adoption of deep learning has been the availability of (open-source) software tools containing robust and well-tested implementations of the main building blocks for defining and learning DNNs [@chen2015mxnet; @abadi2016tensorflow; @paszke2017automatic].

Recently, a new wave of software tools is building up on top of these deep learning frameworks to accommodate modern probabilistic models containing deep neural networks [@tran2016edward; @cabanasInferPy; @tran2018simple; @bingham2018pyro]. These software tools usually fall under the umbrella of the so-called probabilistic programming languages (PPLs) [@gordon2014probabilistic; @ghahramani2015probabilistic], which are programming languages focused on describing general probabilistic models and powered by a general inference engine. Although they have been present in the field of machine learning for many years, this first generation of PPLs was mainly focused on defining a flexible language to express probabilistic models which were more general than the traditional ones usually defined by means of a graphical model [@koller2009probabilistic]. The advent of deep learning and the development of probabilistic models containing DNNs has motivated the development of a new family of PPLs [@tran2016edward; @cabanasInferPy; @tran2018simple; @bingham2018pyro] able to define probabilistic models containing DNNs.

The key data structure in these new PPLs are the so-called a stochastic computational graphs (SCGs) [@schulman2015gradient]. Stochastic computational graphs extends standard computational graphs with stochastic nodes. Stochastic nodes are distributed conditionally on their parents and are represented as circles in the subsequent diagrams. Stochastic computational graphs allow then to define complex functions involving expectations over random variables. Figure [fig:StochasticCG] shows several examples of some simple stochastic computational graphs depending on a parameter vector $\lambda$. Modern PPLs offer a wide and diverse range of probability distributions to define stochastic computational graphs [@dillon2017tensorflow]. And these probability distributions are defined over tensors objects.

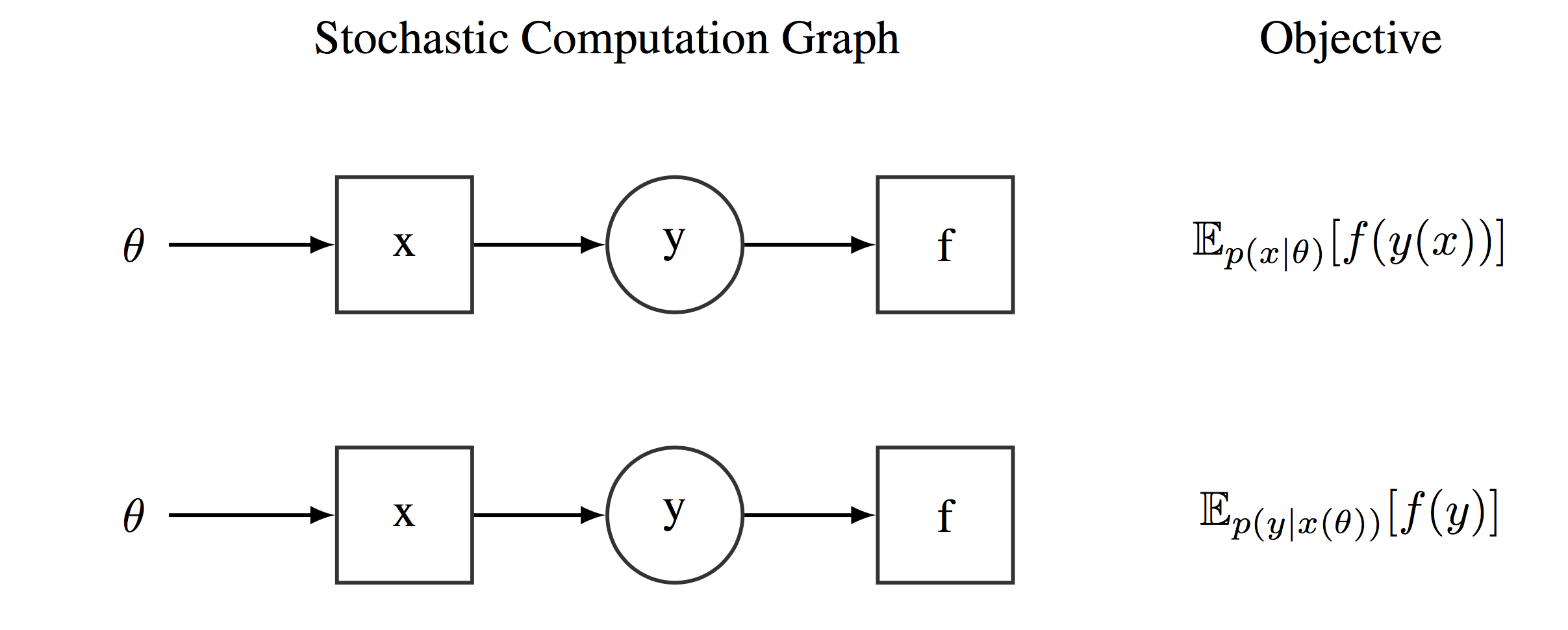[] Examples of two computational graphs encoding two different expectations

We should note that SCGs are not directly implemented within the PPLs, because computing the exact expected value of complex functions is usually not feasible. However, they are indirectly coded on top of the existing computational graph’s framework. In this way, each stochastic node, $\bmz$, is associated with a tensor, $\bmz^\star$, which represents a (set of) sample(s) from the distribution associated to $\bmz$. $\bmz^\star$ is the tensor which is fed to the underlying computational graph. So, SCGs are simulated using standard computational graphs and samples from the defined probability/densities distributions. Figure [fig:EvaluatingStochasticCG] illustrates different possibilities about how SCG can be simulated using standard CGs.

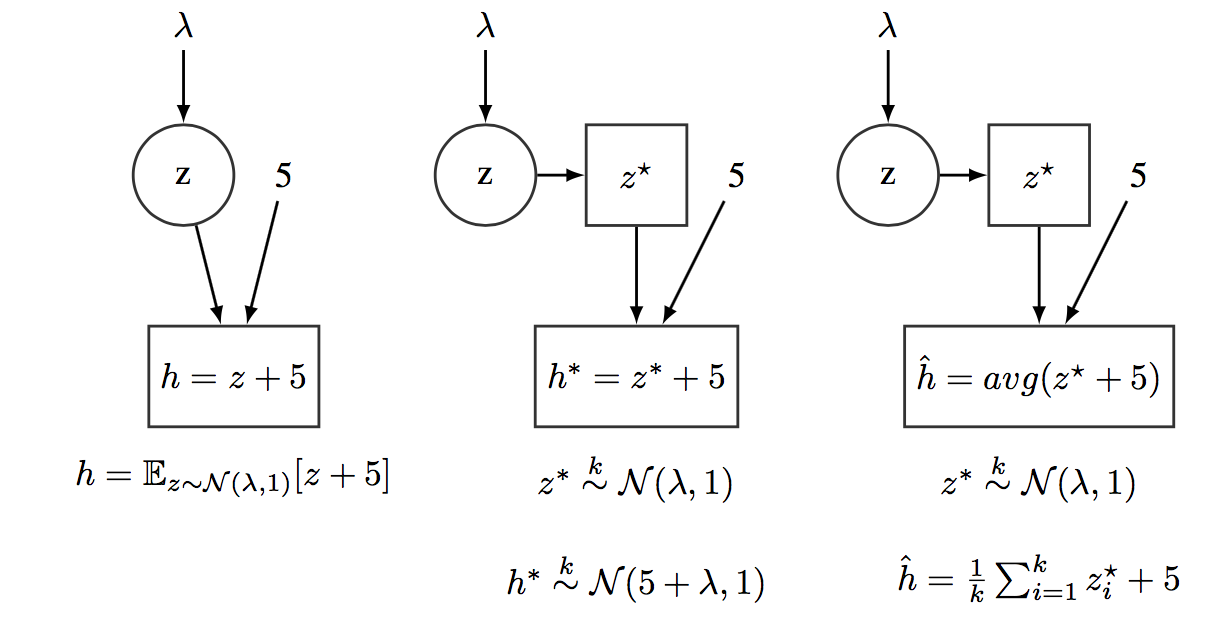[] (Left) A stochastic computational graph encoding the function $h=E_{z}[z + 5]$, where $z\sim N(\lambda,1)$. (Center) Computational graph processing $k$ samples from $z$ and producing $h^\star$ containing $K$ samples from $N(\lambda+5,1)$. (Right) Computational graph processing $k$ samples from $z$ and producing $\hat{h}$, an estimate of $E_z[z + 5]$. Note that CGs efficiently operate with tensors, with current toolbox like Tensorflow exploiting high-performance computing hardware such as GPUs or TPUs. So, its much more efficient to run the CG once over a bunch of samples, than running multiple times the CG over a single sample.

Stochastic computational graphs allow defining quite general probabilistic models, potentially including complex deterministic relationships as DNNs. All the concepts review in this post applies to any probabilistic model which can be defined by means of a stochastic computational graph. Even though, the following equation provides a general characterization covering most of the models discussed in this post in terms of a deep LVM. We introduce this characterization because it will be easier for the reader to trace back a connection with the models and concepts commented in previous posts.

[] \(\begin{aligned} \label{eq:dnnexponentialform} \ln p(\bmbeta) &=& \ln h(\bmbeta) + \bmalpha^T t(\bmbeta) - a_g(\bmalpha)\nonumber\\ \ln p(\bmz_i|\bmbeta) &=& \ln h(\bmz_i) + \eta_z(\bmbeta)^T t(\bmz_i) - a_z(\eta_z(\bmbeta))\nonumber\\ \bmh_0 &=& a_0(\bmz_i^T\bmbeta_0)\nonumber\\ &\ldots &\nonumber\\ \bmh_{l} &=& a_l(\bmh_{l-1}^T\bmbeta_{l-1})\nonumber\\ &\ldots &\nonumber\\ \bmh_L &=& a_L(\bmh_{L}^T\bmbeta_L)\nonumber\\ \ln p(\bmx_i|\bmz_i,\bmbeta) &=& \ln h(\bmx_i) + \eta_x(\bmh_L)^T t(\bmx_i) - a_x(\eta_x(\bmh_L)).\end{aligned}\)

As can be seen, the main difference with respect to standard LVMs is the conditional distribution over the observations $\bmx_i$ given the local hidden variables $\bmz_i$ and the global parameters $\bmbeta$. Now, this conditional relationship is governed by the DNN parameterized by $\bmbeta$. The DNN affects how the hidden variable $\bmz$ defines the parameters of the conditional distribution $p(\bmx\given\bmz)$. Note that the DNN does not directly relate $\bmz$ with $\bmx$. A graphical description of this new model can be found in Figure [fig:DNNModel].

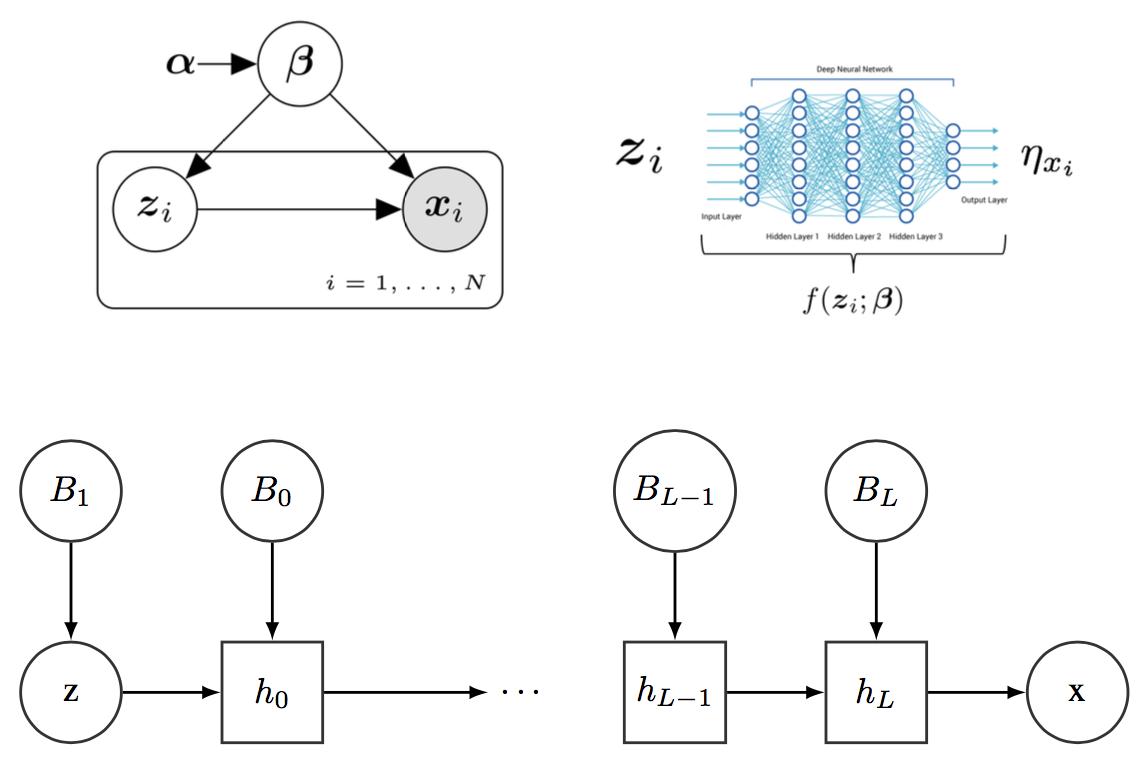[] Core of the probabilistic model examined in this post.

Deep exponential family models [@ranganath2015deep] would be a straightforward extension of this model family which is not covered here. It includes different hierarchies of latent variables which gives rise to a more expressive model family. But all the inference methods revised in this work would apply to these more complex models with minor adaptations.

[]

Example 4: The Generative part of Variational Auto-Encocer

As commented above, Variational Auto-encoders are widely adopted LVM containing DNNs [@kingma2013auto]. Algorithm [alg:vae] provides a simplified pseudo-code description of the generative model of a VAE.

[]

This model is quite similar to the PCA model presented in Example [example:PCA]. The main difference comes from the conditional distribution of $\bmx_i$. In the PCA model, the mean of the Normal distribution of $\bmx_i$ depends linearly on $\bmz_i$ through $\bmbeta$. In the VAE model, the mean depends on $\bmz_i$ through a DNN parametrized by $\bmbeta$, this DNN is known as the decoder network of the VAE [@kingma2013auto]. Note that the original formulation of this model also includes another DNN which connects $\bmz_i$ with the variance of the Normal distribution of $\bmx_i$. It easy to see that this model belongs to the model family described by Equations  [eq:dnnexponentialform].

References